ムラサキツユクサの葉の裏側の表皮細胞です。
右上には、孔辺細胞、その中には葉緑体、孔辺細胞の左隣の細胞には
核がはっきりと映っています。中央左右の細胞には、ミトコンドリアが
映っています。動画では原形質流動など動きがよく分かります。
因みに、自分で撮影したものですよ‼
ESPEKでは、こういうこともやっちゃいます。
サイエンスラボでも見せてますよ‼
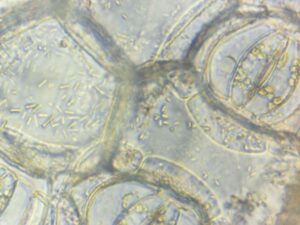
ムラサキツユクサの葉の裏側の表皮細胞です。
右上には、孔辺細胞、その中には葉緑体、孔辺細胞の左隣の細胞には
核がはっきりと映っています。中央左右の細胞には、ミトコンドリアが
映っています。動画では原形質流動など動きがよく分かります。
因みに、自分で撮影したものですよ‼
ESPEKでは、こういうこともやっちゃいます。
サイエンスラボでも見せてますよ‼

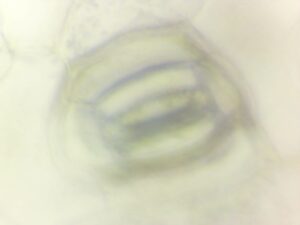
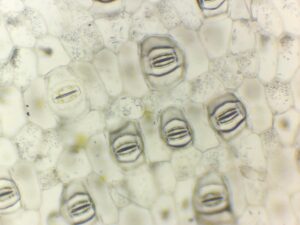
新しいツールで、ムラサキツユクサの気孔(孔辺細胞)
とオオカナダモの表皮細胞を撮影してみました。
7/9(土) 7/10(日)のサイエンスラボでも紹介していきます。




投稿が遅くなりました。
7月のサイエンスラボは、「手作り顕微鏡で細胞を観察しよう‼」です。
7/9(土)・10(日)に行います。座席に限りがありますので、お早めにご予約ください。
今回は、本物の顕微鏡画像との比較もできるようにしました。
前回ご参加いただいた方も楽しめる内容です。

木更津高校の生徒たちから、「必要条件と十分条件がわからない‼」という話が大分出ているので、
考え方を示しておきますね。
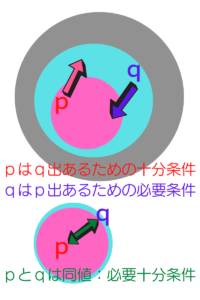
p⇒q が成立するとき、pはqであるための十分条件という。
qはPであるための必要条件という。
p⇔q が成立するとき、qはpであるための必要十分条件という。
そのものなのですが、
実は、条件の包含関係から見た方が判断しやすいです。
命題が真であるためには、図のような包含関係が成立しているはずなので、
条件がどういった包含関係か調べれば一目瞭然のはず‼
演習問題にあてはめて、試してみてください。
きっと正解できると思います。
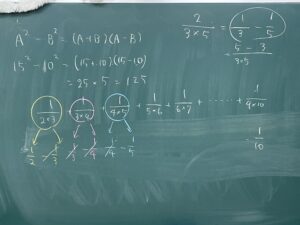

4/27(水)・4/30(土)の2日間 各2時間半、合計5時間にわたって『計算のツボ』フルバージョンを実施しました。小学6年生から、中学3年生までが参加してくれました。ほとんどの生徒が、フルで参加、頭を使った計算ばかり5時間、完走してくれました。
計算の仕方は勿論、勉強の仕方なども話をすることができたので、とても有意義な時間でした。
この講座で習得したことは、必ず今後の数学に生かされるはずです。
学習したことを忘れないでくださいね。
問1 10を最初の数として、偶数を20番目まで足すと合計はいくつですか?
問2 96×21= (暗算)
計算の仕方に興味のある人は、質問してね!
省エネで計算ができるようになると、数学(算数)の問題が早く正確に解けるようになります。
計算のスピードが上がると、入試・模擬試験・定期テストで終わらなかった問題に手が付けられるようになり、自ずと得点が上がります。
例えば、
35 × 35 が いくつになるか直ぐ答えが出せますか?
結構有名な技ですが、知っていれば筆算などせずとも一瞬で答えが出ます。
3 ⋮ 5 × 3 ⋮ 5
↓+1 ↓+0
4 × 3 =12
12の後ろに25をくっ付ければ答えです。
つまり 1225となります。
ですから、

85 × 85 = 9×8のしっぽに25を付けて
7225ですよね。
計算にはこのような小技がたくさんあります。それを覚えていくと、『エレガント』な計算ができるようになっていきます。

特別講座『計算のツボ』 日程:4/27・4/30 17:30~20:00 遅刻・途中退室可(両日参加可)
定員:各日程15名(定員になり次第締め切りとなります)
参加費:無料
対象:小6~中3
申し込み方法:HPの問い合せフォームもしくはお電話にて(0438‐20‐3311)

中3:確認テスト1~4
中2:確認テスト1~4
中1:確認テスト1~4
ノートに解いて、○付けをして、GW明けの初回授業日に提出してね。


中3:テキスト P202・203・206・207・214・215
中2:テキスト P219・220・221・225・226・227
中1:テキスト P34・35・36・37
ノートに解いて、○付けをして、GW明けの初回授業日に提出してね。

今日は、立体図形の基礎についてお話しますね。とても簡単なお話です。
(1)立方体の展開図は全部で何種類ありますか?
(2)(1)で答えた全ての種類の展開図を描いてみてください。 さて、分かりますか?
スラスラ答えられる方は、かなり優秀ですね。
でもね、実は小学校4年生の教科書にバッチリ載っています。そして、これは、高校入試にも、過去に何度も出題された内容なのですよ。
練習して覚えてくださいね。(描いて描いて描きまくってください‼‼‼)


皆さん自転車に乗れますか?失礼な‼乗れるよね。そこで、初めて自転車に(補助なしですよ)乗れるようになった時のことを思い出してください。
すぐに乗れるようになってしまったセンスの良い人はさておいて、大抵の人は、何度も何度も転んだりしながら、膝小僧から流血しながら「どうやったら上手く乗れるかなア」なんて考えながら、チャレンジしたことと思います。あんなに苦労して、乗れるようになってしまったら、何も考えずにスイスイと運転できますよね。これは、全ての事柄に通じます。はじめは、「難しいな」・「嫌だな」・「イライラするな」・「思うようにならない」など、大変だと感じることが多いでしょう。でも、一つ一つ、一歩一歩、丁寧に取り組んでいけば、自転車にスイスイ乗れるように、問題をスラスラ解けるようになるのです。でもね、練習は絶対に必要だし、ごまかしは効かないので、着実に練習してくださいね。
例えば、中学生で方程式の計算がうまく解けない生徒は、文字式の計算や正負の数の計算や、小学校の分数の計算が中途半端にしか理解していないことが多いですし、「方程式の応用が苦手です。」って質問に来る生徒が、実は小学校の割合や速さの計算が理解できていないというケースはよくあります。さて、どうしたら克服できますか?もう皆さんお分かりですよね。つまづいたところに戻って少しやり直してみると良いのです。だから、時間をかける必要がありますよ。人によって克服しなければならないポイントは違うと思います。何をしたらよいかは、私達ESPEK.の教師に聞いてくださいね。一番の近道を誘導します。
諦めてしまったら、そこでおしまいです。諦めずにチャレンジすれば、自転車にスイスイ乗れるようになったようにスラスラ解けるようになりますよ‼





代表の和知です。数学(小4~大学受験)と理科(中1~大学受験)を担当しています。私は5年前から、ランニングを始め、アクアラインマラソンに出場して完走したのを良いことに、トライアスロンにも手を出しています。実は、中学・高校・大学とバリバリの文化部出身なので、運動経験は無いに等しいのです。更に走り始めたときの体重はなんと88kg(現在は72kg)だったのです。マラソンの練習を始めた頃は、100m走るのも息が切れて大変でした。先ずは「10km走れるようになる」という目標を立てましたが、はじめは全く無理だったので、歩くことからスタートしました。10km歩くことが平気になると、次は5km軽くジョギングをして残りを歩く、それに慣れるとジョギングの距離を7kmに増やす・・・というようにゆっくり徐々に距離を延ばしながら、毎日、1ヶ月かけて10km走れるようにしました。一度10km走れるようになると、走る事に関して日々自分が成長している事が楽しくなり、更に練習を積むようになりました。距離も20km位なら平気で走れるようになり、タイムもはじめと比べると大分速くなりました。自信がつくと他のこともやってみたくなり、swimやbikeの練習をしてトライアスロンにチャレンジするようになったのです。トライアスロンという競技は、様々な距離がありますが、比較的ポピュラーなものがオリンピックで行われる、オリンピックディスタンス(swim=1.5km bike=40km run =10km total=51.5km)を走破してタイムを競います。勿論完走してますよ。いい年をしたおじさんでも諦めずに練習を積めばこんな競技に参加できるようになるのです。
実は勉強も同じです。なんで間違えたのか、何で理解できていないのかを考えながら、丁寧に練習を積んでいけば、必ずできるようになります。きっと結果がついてきます。スポーツでも勉強でも、学ぶ上で一番大切なことは、諦めずに愚直なまで練習を積むことです。マラソンという競技、トライアスロンという競技、そして勉強という競技に自分の能力を合わせていく作業が必要になるからです。でも、一番大切なことは練習を積んでいる自分を楽しむポジティブな精神なのかもしれません。私は、これからも様々なことに諦めずにチャレンジし続けたいと考えています。諦めがわるいことは、美徳です。
(減量したい方、一緒に走りませんか??)